These 8 array manipulation techniques in Microsoft Excel will stun you! The 6th is superb.

Excel Arrays are manipulated like Rubik's Cube Puzzles

Did you ever search for examples of Excel array manipulation techniques? You might have found some but none of which applies to financial reporting. In this article, we will delve into the techniques I exploited to solve my eight profit formula challenges, which I earlier posted at Microsoft Excel Tech Community and shared at LinkedIn. To my surprise, only Mark Robson had a tolerable solution!

The Rules of the Challenge

The Challenge entails the construction of formulas starting in N11 that return the results starting in M11, subject to these rules:

Requirements and Rules of Profit Formula Challenge

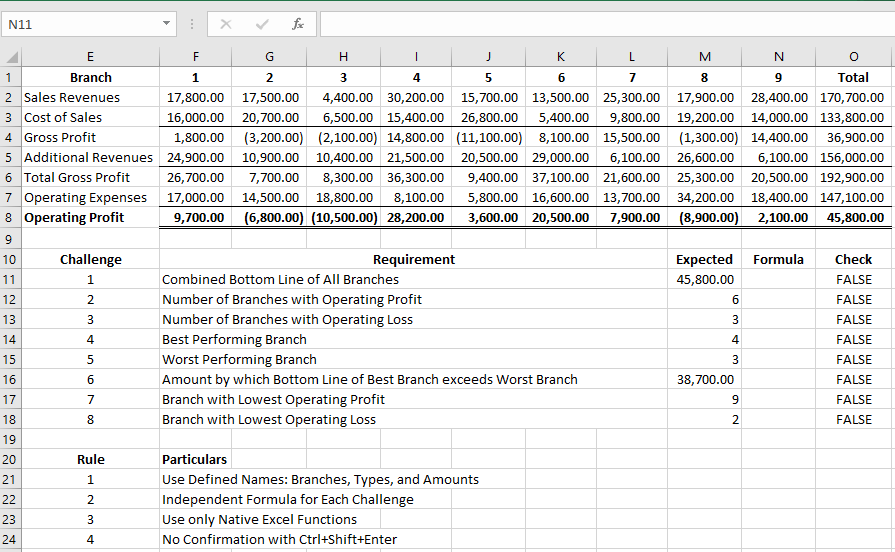
1. No other names must be used, except those which are already defined as Branches, Types, and Amounts;

2. Each formula must not refer to any result returned by the other formulas;

3. No user-defined-functions are allowed; and

4. Each formula must be confirmed with ENTER only, regardless of the Excel version of the user.

Challenge 1: The Combined Bottom Line of All Branches

To return the Combined Bottom Line of All Branches, we subtract Twice the Total Cost of Sales and Total Operating Expenses from the Total Amounts by wrapping SUMIF with SUM, as follows:

=SUM(Amounts,
-2*SUMIF(Types,{"c*","o*"},
Amounts))

In the formula above, SUMIF evaluates to:

=SUM(Amounts,
-2*{133800,147100})

Finally, SUM returns the required result, as follows:

=45800

The array creation formula is stunning

The Creation of the Array for Manipulation

For Challenges 2 to 8, we first create this array that we will later manipulate to return each of the required results:

=MMULT(SUMIFS(Amounts,
Types,{"s*","c*","a*","o*"},
Branches,ROW(1:9)),{1;-1;1;-1})

The formula above uses these functions:

1. ROW returns a 9-row by 1-column array;

2. SUMIFS returns a 9-row by 4-column array; and

3. MMULT returns a 9-row by 1-column array.

First, ROW returns the Branch Numbers 1 to 9, as follows:

=MMULT(SUMIFS(Amounts,
Types,{"s*","c*","a*","o*"},
Branches,{1;2;3;4;5;6;7;8;9}),{1;-1;1;-1})

Next, SUMIFS returns the Sums of each Line Item per Branch, as follows:

=MMULT({17800,16000,24900,17000;17500,20700,10900,14500;4400,6500,10400,18800;30200,15400,21500,8100;15700,26800,20500,5800;13500,5400,29000,16600;25300,9800,6100,13700;17900,19200,26600,34200;28400,14000,6100,18400},{1;-1;1;-1})

Finally, MMULT returns the Bottom Lines of each Branch, as follows:

={9700;-6800;-10500;28200;3600;20500;7900;-8900;2100}

In the succeeding sections, we will manipulate the array above to return the result required for each individual challenge!

Challenge 2: The Number of Branches with Operating Profit

To return the Number of Branches with Operating Profit, we wrap the equivalent numbers of the logical values with SUMPRODUCT, as follows:

=SUMPRODUCT(--(MMULT(SUMIFS(Amounts,
Types,{"s*","c*","a*","o*"},
Branches,ROW(1:9)),{1;-1;1;-1})>0))

In the formula above, we first determine whether each value in our array is more than zero, as follows:

=SUMPRODUCT(--({9700;-6800;-10500;28200;3600;20500;7900;-8900;2100}>0))

The comparison above evaluates to this array of logical values:

=SUMPRODUCT(--({TRUE;FALSE;FALSE;TRUE;TRUE;TRUE;TRUE;FALSE;TRUE}))

The double negatives converts the logical values to their number equivalents, as follows:

=SUMPRODUCT({1;0;0;1;1;1;1;0;1})

Finally, SUMPRODUCT returns the required result, as follows:

=6

Although four characters longer, this combination of INDEX and FREQUENCY impressively returns the same result:

The INDEX-FREQUENCY combination is impressive

=INDEX(FREQUENCY(MMULT(SUMIFS(Amounts,
Types,{"s*","c*","a*","o*"},
Branches,ROW(1:9)),{1;-1;1;-1}),0),2)

In the formula above, FREQUENCY evaluates to:

=INDEX({3;6},2)

Finally, INDEX returns the required result, as follows:

=6

Challenge 3: The Number of Branches with Operating Loss

To return the Number of Branches with Operating Loss, we simply modify the comparison operator in our Challenge 2 Formula from more than to less than, as follows:

=SUMPRODUCT(--(MMULT(SUMIFS(Amounts,
Types,{"s*","c*","a*","o*"},
Branches,ROW(1:9)),{1;-1;1;-1})<0))

Similar to Challenge 2, the comparison above evaluates to this array of number equivalents of the logical values:

=SUMPRODUCT({0;1;1;0;0;0;0;1;0})

Finally, SUMPRODUCT returns the required result, as follows:

=3

Using the combination of INDEX and FREQUENCY, we simply modify row_num from 2 to 1, as follows:

=INDEX(FREQUENCY(MMULT(SUMIFS(Amounts,
Types,{"s*","c*","a*","o*"},
Branches,ROW(1:9)),{1;-1;1;-1}),0),1)

Similarly, the formula above returns the required result, as follows:

=3

Challenge 4: The Best Performing Branch

To return the Number of the Best Performing Branch, we determine the Branch Number corresponding to the Highest Operating Profit, as follows:

The LOOKUP-FREQUENCY combination is magical

=LOOKUP(2,1/FREQUENCY(-9.9E+307,-MMULT(SUMIFS(Amounts,
Types,{"s*","c*","a*","o*"},
Branches,ROW(1:9)),{1;-1;1;-1})),ROW(1:9))

In the formula above, FREQUENCY returns a vertical array of numbers through these procedures:

1. Precede bins_array with negative sign so that the signs of the values in our array will be interchanged; and

2. Use the largest negative number as data_array so that it will be included in the count of the lowest number in the bins_array.

After the first procedure above, bins_array evaluates to:

=LOOKUP(2,1/FREQUENCY(-9.9E+307,{-9700;6800;10500;-28200;-3600;-20500;-7900;8900;-2100}),ROW(1:9))

Next, FREQUENCY returns this vertical array of 1 and 0's:

=LOOKUP(2,1/{0;0;0;1;0;0;0;0;0;0},ROW(1:9))

In the formula above, LOOKUP returns the Number of the Best Performing Branch through these procedures:

1. Use ROW as result_vector so that it will return the numbers 1 to 9;

2. The number 1 is divided by the values in our array so that lookup_vector will evaluate to an array of 1 and #DIV/0! errors; and

3. Use 2 as lookup_value so that it will match the position of 1 in lookup_vector.

After the first procedure above, result_vector evaluates to:

=LOOKUP(2,1/{0;0;0;1;0;0;0;0;0;0},{1;2;3;4;5;6;7;8;9})

After the second procedure above, lookup_vector evaluates to:

=LOOKUP(2,{#DIV/0!;#DIV/0!;#DIV/0!;1;#DIV/0!;#DIV/0!;#DIV/0!;#DIV/0!;#DIV/0!;#DIV/0!},{1;2;3;4;5;6;7;8;9})

Finally, LOOKUP returns the required result, as follows:

=4

Challenge 5: The Worst Performing Branch

To return the Number of the Worst Performing Branch, we determine the Branch Number corresponding to the Highest Operating Loss, as follows:

=LOOKUP(2,1/FREQUENCY(-9.9E+307,MMULT(SUMIFS(Amounts,
Types,{"s*","c*","a*","o*"},
Branches,ROW(1:9)),{1;-1;1;-1})),ROW(1:9))

Except for the omission of the negative sign preceding bins_array, the formula above is the same as our solution to Challenge 4. Thus, bins_array evaluates to:

=LOOKUP(2,1/FREQUENCY(-9.9E+307,{9700;-6800;-10500;28200;3600;20500;7900;-8900;2100}),ROW(1:9))

Next, FREQUENCY returns this vertical array of 1 and 0's:

=LOOKUP(2,1/{0;0;1;0;0;0;0;0;0;0},ROW(1:9))

Finally, LOOKUP returns the required result, as follows:

=3

Challenge 6: The Amount by which the Bottom Line of the Best Performing Branch exceeds the Bottom Line of the Worst Performing Branch

To return the Amount by which the Bottom Line of the Best Performing Branch exceeds the Bottom Line of the Worst Performing Branch, we use the combination of MMULT and AGGREGATE, as follows:

The MMULT-AGGREGATE combination is superb

=MMULT({1,-1},AGGREGATE({14;15},4,MMULT(SUMIFS(Amounts,
Types,{"s*","c*","a*","o*"},
Branches,ROW(1:9)),{1;-1;1;-1}),1))

In the formula above, AGGREGATE returns the Bottom Lines of the Best and the Worst Performing Branches, as follows:

=MMULT({1,-1},{28200;-10500})

Finally, MMULT returns the Difference between those two Bottom Lines, as follows:

=38700

Challenge 7: The Branch with Lowest Operating Profit

To return the Number of the Branch with Lowest Operating Profit, we determine the Branch Number corresponding to the Lowest Operating Profit, as follows:

=LOOKUP(2,1/FREQUENCY(0,MMULT(SUMIFS(Amounts,
Types,{"s*","c*","a*","o*"},
Branches,ROW(1:9)),{1;-1;1;-1})),ROW(1:9))

Except for the modification of data_array from -9.9E+307 to 0, the formula above is the same as our solution to Challenge 5. Thus, FREQUENCY returns this vertical array of 1 and 0's:

=LOOKUP(2,1/{0;0;0;0;0;0;0;0;1;0},ROW(1:9))

Finally, LOOKUP returns the required result, as follows:

=9

Challenge 8: The Branch with Lowest Operating Loss

To return the Number of the Branch with Lowest Operating Loss, we determine the Branch Number corresponding to the Lowest Operating Loss, as follows:

=LOOKUP(2,1/FREQUENCY(0,-MMULT(SUMIFS(Amounts,
Types,{"s*","c*","a*","o*"},
Branches,ROW(1:9)),{1;-1;1;-1})),ROW(1:9))

Except for the modification of data_array from -9.9E+307 to 0, the formula above is the same as our solution to Challenge 4. Thus, FREQUENCY returns this vertical array of 1 and 0's:

=LOOKUP(2,1/{0;1;0;0;0;0;0;0;0;0},ROW(1:9))

Finally, LOOKUP returns the required result, as follows:

=2

Copy of the Solution File

Were you stunned? Kindly inform me of your thoughts on the solution file through a comment below.